機械学習の基本である線形回帰のコードを書いてみます。
流れの説明:
1) データファイルの読み込み:
データファイルはtextデータで
x0, y0
x1, y1
...
のように格納しています。
今回以下のような ダミーの(身長, 体重)データを使用しました.
85, 16.8
90.5, 17.2
100.0, 17.5
110.3, 18.9
116.5, 21.4
122.5, 27.2
128.2, 30.5
133.5, 34.2
139.0, 38.2
145.0, 44.0
152.8, 49.0
160.0, 53.9
165.3, 58.9
168.2, 60.6
169.9, 62.6
2) データの標準化
読み込んだデータをパラメータの収束を早めるために標準化します。
ここでは、データの平均をゼロ、標準偏差を1にするように標準化します。
3) 線形fittingの実行
x = 身長
y = 体重
として、
線形関数
y = t0 + t1 * x
でデータをfittingします。
具体的には、パラメータt0, t1をすこしずつ変化させながら、最小2乗誤差
E = 0.5 ( y_予想 - y_正解)^2
が最小になる場所を求めます。
Eが最小になる場所ではEのt0, t1の微分がゼロになることから、パラメータを変化させたときのEの変化が小さくなったらEのlocal minimumになったと判定して、パラメータ更新のループを終了させます。
パラメータの更新の方法は勾配降下法を採用します。これは、誤差関数をパラメータで微分してその点での傾きに応じて傾きの方向に徐々に勾配を下っていくという方法です。
パラメータと誤差の変化の途中経過は毎ループprintするようにします。
4) 結果をグラフに書く
最後に、元のデータとfitting結果をグラフに描画します
以上の内容を具体的にPythonのコードで書いたものが以下になります.
###############
# 線形回帰の実装
###############
import numpy as np
import matplotlib.pyplot as plt
### (1) データ読み込み ###
trainData = np.loadtxt('kodomoShinchouTaijyu.txt', delimiter=',', skiprows=0)
trainDataX = trainData[:, 0]
trainDataY = trainData[:, 1]
#plt.plot(trainDataX, trainDataY, 'o')
#plt.show()
### (2) データの標準化
mu = trainDataX.mean() # 平均
sigma = trainDataX.std() # 標準偏差
def standaradize(x):
return (x - mu)/sigma
trainDataXSTD = standaradize(trainDataX)
#plt.plot(trainDataXSTD, trainDataY, 'o')
#plt.show()
### 線形fitting ###
# fitting関数 (線形回帰)
def f(x):
return t0 + t1 * x
# MSE関数(最小2乗の損失関数)
def E(x, y):
return 0.5 * np.sum( (y - f(x)) ** 2)
### 学習 ###
ncount = 0 # 更新回数
eta = 1e-2 #学習率
diff = 1 # 誤差
# パラメータの初期値
t0 = np.random.rand()
t1 = np.random.rand()
# 学習する
error = E(trainDataXSTD, trainDataY)
while diff > 1e-3: # 損失関数の変化が小さくなるまでループする
# 勾配降下法の実行
tmp0 = t0 - eta * np.sum( (f(trainDataXSTD) - trainDataY))
tmp1 = t1 - eta * np.sum( (f(trainDataXSTD) - trainDataY) * trainDataXSTD)
t0 = tmp0
t1 = tmp1
# 1つ前のステップの誤差との差分
currentError = E(trainDataXSTD, trainDataY)
diff = error - currentError
error = currentError[f:id:wshinya:20180325141117p:plain]
# 途中経過を出力
ncount += 1
log = '{}: t0 = {:.3f} t1 = {:.3f}, diff={:.4f}'
print(log.format(ncount, t0, t1, diff) )
### 結果をグラフにする
x = np.linspace(-2, 2, 100)
plt.plot(trainDataXSTD, trainDataY, 'o')
plt.plot(x, f(x))
plt.show()
上記コードを実行すると、私の環境ですと48回のイテレーションで結果が収束し、以下のようなグラフが表示されました。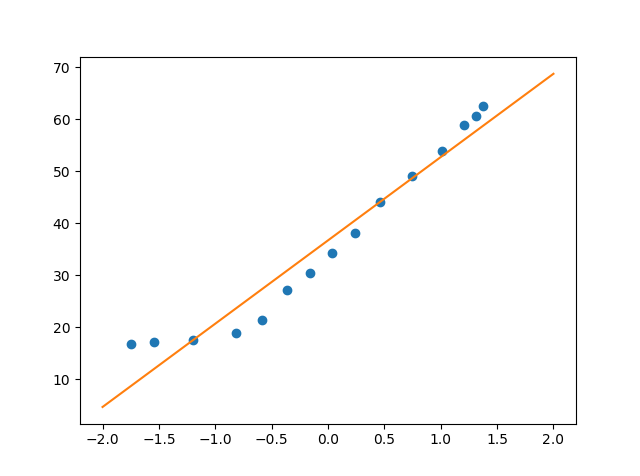
身長が小さい時にあえて線形からずれるようにデータを作りましたのでxが小さい時にだいぶずれていますね。
それから、横軸は標準化したままのデータを描画しています。